提到行测排列组合题目,考生们第一反应就是“难”,第二反应就是放弃。但如果在平时备考中能掌握一些常用的解题方法,勤加练习,在真正的考场上是可以尝试去做,让自己更上一层楼的。接下来给大家介绍三种常用方法。
一、优限法
适用环境:题干中出现有绝对限制条件的元素或者位置时,考虑用优限法。
具体操作:优先安排有限制条件的元素或者位置,再安排其他元素或者位置。
【例1】一次会议某单位邀请了10名专家,该单位预定了10个房间,其中一层5间、二层5间。已知邀请专家中4人要求住二层、3人要求住一层、其余3人住任一层均可。那么要满足他们的住房要求且每人1间,有多少种不同的安排方?
A.75
B.450
C.7200
D.43200
答案:D
【解析】本题中要将10名专家安排到10个房间,且每间安排一人。在安排过程中提到两个要求:1.4人要求住2层,2.3人要求住1层。这两个要求就体现了我们说的“有绝对限制条件的元素”。因此我们考虑用优限法解决。共有10人,其中4人要求住2层,从二层的5个房间中选出4个,安排4人入住,其方法数为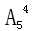 ,3人要求住一层,从一层的5个房间中选出3个,安排3人入住,其方法数为
,3人要求住一层,从一层的5个房间中选出3个,安排3人入住,其方法数为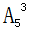 ,其余3人安排住剩下的3个房间,其方法数为
,其余3人安排住剩下的3个房间,其方法数为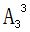 ,故共有
,故共有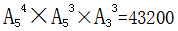 种不同的安排方案。
种不同的安排方案。
二、捆绑法
适用环境:题干中要求元素相邻或者位置相邻时,考虑捆绑法。
具体操作:先考虑整体的顺序要求,再考虑整体内部的顺序要求。
【例2】为加强机关文化建设某市直机关在系统内举办演讲比赛3个部门分别派出3、2、4名选手参加比赛,要求每个部门的参赛选手比赛顺序必须相连,问不同的参赛顺序的种数在以下哪个范围之内?
A小于1000
B1000-5000
C.5001-20000
D.大于20000
答案:B
【解析】本题中要安排3个部门中参赛选手的演出顺序。在安排过程中要求每个部门的参赛选手比赛顺序必须相连。这个要求体现了我们说的“元素相邻”,考虑用捆绑法,首先将三个部门的选手看成3个整体,考虑三个整体的出场顺序,有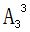 =6种;其次考虑每个整体内选手的出场顺序,分别有
=6种;其次考虑每个整体内选手的出场顺序,分别有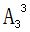 =6种,
=6种,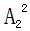 =2种,
=2种,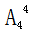 =24种。则不同参赛顺序的种数为6×6×2×24=1728,计算结果显然大于1000小于5000,故此题答案为B。
=24种。则不同参赛顺序的种数为6×6×2×24=1728,计算结果显然大于1000小于5000,故此题答案为B。
三、插空法
适用环境:题干中要求元素不相邻时,考虑插空法。
具体操作:先安排其他元素的位置,再将不相邻的元素插空安排。
【例3】由数字1、2、3、4、5组成无重复数字的五位数,两个偶数互不相邻的五位数有几个?
答案:72个
【解析】本题中要用1-5个组成无重复数字的五位数,组数过程中要求两个偶数互不相邻,这提现了我们说的“要求元素不相邻”,考虑用插空法。先安排剩余的3个奇数,有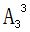 =6种,在从奇数形成的4个空位里选2个空将剩余的2个偶数放入,有
=6种,在从奇数形成的4个空位里选2个空将剩余的2个偶数放入,有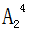 =12种,因此所求为6×12=72个。
=12种,因此所求为6×12=72个。
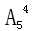 ,3人要求住一层,从一层的5个房间中选出3个,安排3人入住,其方法数为
,3人要求住一层,从一层的5个房间中选出3个,安排3人入住,其方法数为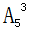 ,其余3人安排住剩下的3个房间,其方法数为
,其余3人安排住剩下的3个房间,其方法数为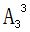 ,故共有
,故共有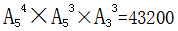 种不同的安排方案。
种不同的安排方案。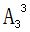 =6种;其次考虑每个整体内选手的出场顺序,分别有
=6种;其次考虑每个整体内选手的出场顺序,分别有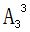 =6种,
=6种,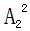 =2种,
=2种,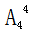 =24种。则不同参赛顺序的种数为6×6×2×24=1728,计算结果显然大于1000小于5000,故此题答案为B。
=24种。则不同参赛顺序的种数为6×6×2×24=1728,计算结果显然大于1000小于5000,故此题答案为B。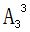 =6种,在从奇数形成的4个空位里选2个空将剩余的2个偶数放入,有
=6种,在从奇数形成的4个空位里选2个空将剩余的2个偶数放入,有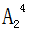 =12种,因此所求为6×12=72个。
=12种,因此所求为6×12=72个。