求解资料分析题目可能涉及的容斥问题多为二者容斥和容斥极值两类，公式如下：

　　二者容斥：I=A+B–A∩B+M

　　容斥极值：(A∩B)min=A+B–I

　　二、例题分析

　　例1、调查显示，关于家庭存书共享意愿的问题，选择“无条件愿意”“有条件愿意”“不愿意”“不知道/不清楚”的受访市民所占比重分别是60.8%、15.1%、20.6%、3.5%。

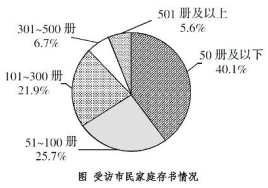
　　选择“无条件愿意”共享家庭存书的受访市民中，一定有人的家庭存书为：

　　A.50册及以下 B.51-100册 C.101-300册 D.301册及以上

　　【答案】A。解析：由文字可知，选择“无条件愿意”的受访市民所占比重是60.8%，由饼状图可知受访市民家庭存书情况中50册及以下的比重为40.1%，因为60.8%+40.1%>100%，所以两者交集必有重合部分，故答案选A。

　　例2、某研究机构从全国随机抽取10个市的儿童家长，对其进行“我国儿童校外生活状况”的问卷调查，回收有效问卷15000份。调查结果显示：对儿童校外生活表示“很重视”的家长占85%以上，表示“很满意”或“比较满意”的占60%。

　　问题：对儿童校外生活表示“很满意”或“比较满意”的家长中，表示“很重视”的家长占比可能是( )。

　　A.53% B.58% C.63% D.78%

　　【答案】D。解析：对儿童校外生活表示“很重视"的家长占85%以上，表示“很满意”或“比较满意"的占60%。根据容斥极值原理可知，既对儿童校外生活表示“很满意"或“比较满意”，又表示“很重视”的家长，这两种属性都具备的那部分人群占所有家长人数的比重至少应大于85%+60%-100%=45%。问题在求这两者属性都具备的家长占表示“很满意”或“比较满意”的家长的比重，则可以用两者交集的最小值除以表示“很满意”"比较满意"的家长的占比，结果应大于45%÷60%=75%。只有D项符合。

　　通过以上几道题目的展示，相信大家对于利用容斥原理解决复杂资料分析题目有了一定的认识，在此基础上大家可以多加练习，熟能生巧。