一、什么是混合比值问题

　　1、资料分析中的比值

　　在资料分析中，常考察　

　　2、比值如何混合

　　以平均分为例，全班女生的

　　可以看到：全班平均分的分子为女生和男生分子之和，分母也为女生和男生分母之和。

　　如果把全班的平均分称为整体比值，女生的平均分和男生的平均分称为部分比值。整体比值的分子为两个部分比值的分子之和，分母为两个部分比值的分母之和。像存在以上这种加和关系的题目，就属于混合比值问题，可以应用十字交叉法来求解。

　　二、如何应用十字交叉法

　　应用十字交叉法需要记住三点规律：

　　1、整体比值介于部分比值之间;

　　2、整体比值更靠近分母较大的部分比值;

　　3、比值交叉作差后的结果之比为分母之比。

　　下面通过例题进行讲解说明。

　　例1、2013年全国中高等学校在校博士生为283810人，其中少数民族学生所占的比重为5.23%;在校硕士生为1436008人，其中少数民族学生所占比重为5.89%。

　　问题：2013年全国中高等学校研究生中，少数民族研究生所占比重约为：

　　A.5.23% B.5.38% C.5.56% D.5.78%

　　【答案】D。解析：这道题研究的是比重。由材料可知，博士中少数民族占比为5.23%，硕士中少数民族占比为5.89%，所求为研究生中少数民族占比，为三个比值，且这三个比值符合分母间、分子间的加和关系，即：研究生=博士生+硕士生，研究生少数民族人数=博士生少数民族人数+硕士生少数民族人数，故可用十字交叉法求解。所求即为整体比值，由第一点规律可知整体比值介于部分比值之间，即所求介于5.23%和5.89%之间，排除A项。进一步应用第二点规律：整体比值更靠近分母较大的部分比值，该题两个部分比值分母分别为在校博士生数量和在校硕士生数量，由材料可知：2013年全国中高等学校在校博士生为283810人，在校硕士生为1436008人，283810<1436008，故所求更靠近硕士中少数民族的占比(5.89%)，即大于(5.23%+5.89%)÷2=5.56%，选择D项。

　　例2、2017年9月，广东省进出口总额同比增长8.1%，其中，进口额同比增长14.2%，出口额同比增长4.5%。

　　问题：2016年9月，广东省出口额约是进口额的多少倍?

　　A.1.2 B.1.5 C.1.7 D.2.4

　　【答案】C。解析：所求为是

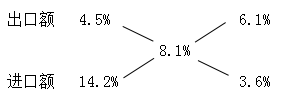
　　由十字交叉法的模型可得，所求为：

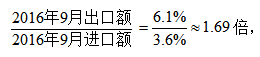
　　相信通过以上两道题目，大家已经对十字交叉法解决混合比值问题有所了解，但熟练地应用建立在大量的练习基础上，希望各位考生备考期间多多做题，提升这类问题的解题能力。