一、知识铺垫

　　容斥问题研究的是集合之间的交叉关系，对于容斥问题的解题原则，我们总结了四个字：“不重不漏”，即“每个区域的元素只算一次”。

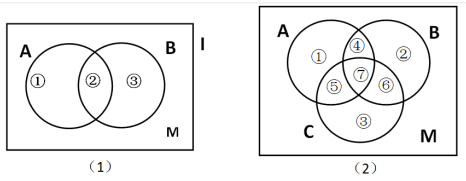
　　如图(1)所示，A、B两个集合之间的交叉关系为二者容斥问题，“不重不漏”就是把①、②、③及M四个区域各算一次，总结为公式：

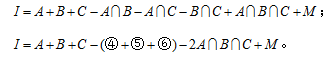
　　二、例题展示

　　例1、工厂组织职工参加周末公益劳动，有80%的职工报名参加。其中报名参加周六活动的人数与报名参加周日活动的人数比为2：1，两天的活动都报名参加的人数为只报名参加周日活动的人数的50%。问未报名参加活动的人数是只报名参加周六活动的人数的：

　　A.20% B.30% C.40% D.50%

　　【答案】C

　　【解析】设两天的活动都报名参加的人数为x，则只报名参加周日活动的人数为2x，由“报名参加周日活动的人数等于两天的活动都报名参加的人数与只报名参加周日活动的人数之和”，可得报名参加周日活动的人数为3x，根据“报名参加周六活动的人数与报名参加周日活动的人数比为2：1”，可得报名参加周六活动的人数为6x，从而只报名参加周六活动的人数为5x，那么报名参加活动的总人数为：2x+5x+x=8x，由于“有80%的职工报名参加”，所以工厂职工总数为：8x÷80%=10x，那么未报名参加活动的人数为：10x-8x=2x，所求是：2x÷5x=40%。故答案选C。

　　例2、有100人参加运动会的三个比赛项目，每人至少参加一项，其中未参加跳远的有50人，末参加跳高的有60人，未参加赛跑的有70人。问至少有多少人参加了不止一个项目?

　　A.7 B.10 C.15 D.20

　　【答案】B

　　【解析】根据“有100人参加运动会的三个比赛项目，每人至少参加一项”可知这100人中没有不参加运动会的人，由“其中未参加跳远的有50人，末参加跳高的有60人，未参加赛跑的有70人”可分别得出：参加跳远的有50人，参加跳高的有40人，参加赛跑的有30人。设参加两项的有x人，参加三项的有y人，根据三者容斥公式可得：50+40+30-x-2y=100，解得x+2y=20。所求为：“至少有多少人参加了不止一个项目”，即求的是x+y的最小值。由x+y=20-y，可知要想求出x+y的最小值，就要使y尽可能大，当x为0时，y取最大值为10，所以求出x+y的最小值是：20-10=10。故答案选B。

　　通过这两道例题我们可以发现只要分析好题干中各个集合所代表的具体含义，进一步分析并利用公式就可以帮助求解一般的容斥问题，希望各位同学多加练习此类题目并加以总结，真正理解容斥问题的“真面目”。