一、等差数列

　　例1、108，122，143，165，( )

　　A.176 B.188 C.192 D.206

　　【答案】B。解析：数列单调递增，且从大数字看变化幅度2倍左右，可优先考虑作差。但此题作差并非常规思路，而是需要从第二项起，每一项都减去第一项，得到新数列：14、35、57，再进行作差：

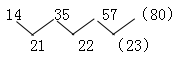
　　题干应填入108+80=(188)。答案选B。

　　例2、168，183，195，210，( )

　　A.213 B.215 C.223 D.225

　　【答案】A。解析：数列单调递增，且从大数字看变化幅度2倍左右，可优先考虑作差：

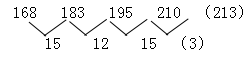
　　如果按照15、12 循环数列规律来计算应为(222)，但没有答案，因此需要换种思路把差数列和原数列结合构造网络，即：15=1+6+8，12=1+8+3，15=1+9+5，(3)=2+1+0，题干应填入210+3=(213)。答案选A。

　　二、和数列

　　例题、1，3，8，15，( )

　　A.22 B.26 C.28 D.24

　　【答案】D。解析：数列单调递增，整体变化幅度2倍左右，且小数字居多，故考虑作和。但此题加和属于非常规思路，是第一项和后面每一项相加后构成了平方数列。即：

　　，故选D。

　　三、组合数列

　　例1、2，12，6，30，25，100，( )，( )

　　A.64，192 B.48，144 C.96，192 D.32，96

　　【答案】A。解析：数列较长，总项数≥7项，优先考虑组合数列。将数列两两分组，每组作商后得到6、5、4、(3)，即所选的两个数字之间是3倍关系，排除C项;此时规律不易发现，需要换种思路把商数列和原数列结合构造网络去探索就会发现：前一组的商与后一组的第一项构成多次方关系，即：

　　。故选A。

　　例2、6，24，8，4，20，10，3，6，( )

　　A.6 B.9 C.12 D.18

　　【答案】A。解析：数列较长，总项数≥7项，优先考虑组合数列。将数列中每三个数作为一组，中间的数为两边数的最小公倍数，只有A 项符合。

　　四、数位组合

　　例题、12，1112，3112，211213，( )

　　A.312213 B.132231 C.112233 D.332211

　　【答案】A。解析：数列具有单调性，从大数字看变化幅度陡增，常规思路易联想到乘积数列或多次方数列，但都无法求解，所以此题规律比较特殊，它是一种规律描述的体现，而非常规的数字计算。即：后一个数是对前一个数的描述，例如：“1112”的意思是：“12”有“1 个1 和1 个2”，依次类推，211213 有3 个1、2 个2、1 个3，即312213。故选A。

　　以上就是行测数字推理中的一些较特殊规律的题目，你掌握了吗?