什么是相对面法?如何运用相对面法?

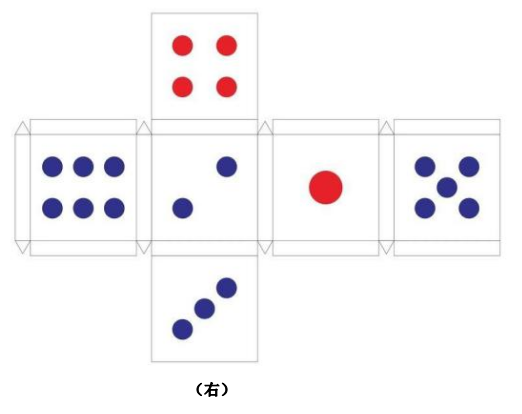
　　骰子是生活中常见的六面体物件(图左)，观察其外观可知，六面体当中任意一个面分别与四个面相接，与另一个面相对，即存在三组相对的面。

　　再看看其展开图(图右)，观察可知折叠之后点3与点4会成为相对的两个面，再结合其立体图左图可知，当能看见点4时，点3不能被看见(图1)，当能看见点3时，点4不能被看见(图2)，也就说明，在立体图的任意平面视角当中，成相对关系的两个面不能同时被看见，若出现此情况则该立体图绝不是相应展开图的折叠立体图，由此可判定选项正误。

　　那么问题来了，如何在展开图当中快速确定相对面呢?很简单，掌握两点即可:

　　①先看行或列，行或列间隔一个面的两个面就是相对面。例如在下图第二行上，面2与面4相隔一个面3，则面2、4为相对面，同理的还有面3、5。

　　②再看“Z”字型，“Z”字型的两端是相对面。例如下图中标记出的“Z”型线状图，其首位两端的面1和面6就是相对面。因此下图展开图的三对相对面为：2与4、3与5、1与6。

　　接着结合例题实战一下。

　　【例1】左边是纸盒外表面的展开图，右边哪一项能由它折叠而成?

　　【解析】六面体折叠问题分三步，①：给题干标号，接着观察其相对面，发现2与4、3与5、1与6成相对面(2与4、3与5相隔一个面，1与6在“Z”字两端);②：观察是否有相同面，发现3与5、1与6相同(观察相同面是为了后续准确地给选项定面);③：定面分析选项。如图，给选项定面后发现ABC项均出现了一组相对面，相对面在立体图当中不能同时被看到，因此ABC项一定不能由题干展开图折叠而成，排除，故本题答案为D项。

　　【例2】把下面的六个图形分为两类，使每一类图形都有各自的规律()。

　　A.①③④，②⑤⑥

　　B.①③⑤，②④⑥

　　C.①②⑤，③④⑥

　　D.①④⑥，②③⑤

　　【解析】观察可知六个图形均为六面体的展开图，且每个展开图均是由三个黑面和三个白面组成，要将其分成两组，可以观察黑面(白面)之间的位置关系，仔细观察可发现(如下图)：

　　图③④⑥当中均出现一组黑色相对面，而图①②⑤当中的黑面不存在相对关系，据此可分成两组，故本题答案为C项。(此题虽是分类题，但实际是在考察六面体的基本性质，可见六面体的出题形式并不单一)

　　可以看出，折叠问题技巧性很高，不需要靠想象便能高效解题，掌握相应技巧便能用于六面体的各种题型当中。当然，除了相对面法，还有其他巧妙的方法，感兴趣的同学可以下来多多积累，让六面体不再是难题。